คณิตศาสตร์เสริม

…….ร้อยละที่ใช้อยู่ในชีวิจประจำวันมีมากมาย เช่น อัตราดอกเบี้ยเงินกู้ – เงินฝาก , ลดราคาสินค้า เป็นต้น แต่การคิดร้อยละต้องระบุจำนวนด้วยว่าเป็นร้อยละของจำนวนใด มิฉะนั้น จะได้ผลที่ไม่ถูกต้อง เช่น ร้อยละ 5 หรือ 5% ซึ่งไม่สามารถบอกได้ว่าเป็นร้อยละ 5 ของจำนวนใด
…….แต่ถ้าระบุว่า ร้อยละ 5 ของ 40 หรือ 5% ของ 40 จะหมายถึง $\frac{5}{100}\times 40 = 2$
…….นั่นคือ ร้อยละ 5 ของ 40 เท่ากับ 2
…….หรือ ร้อยละ 5 ของ 75 หมายถึง $\frac{5}{100}\times 75 = 3.75$
…….หรือ ร้อยละ 5 ของ 120 หมายถึง $\frac{5}{100}\times 120 = 6$

ตัวอย่างที่ 1 400% ของ 0.065 มากกว่าหรือน้อยกว่า 4% ของ 650 อยู่เท่าไร
วิธีทำ……. 400% ของ 0.065 หมายถึง $\frac{400}{100}\times 0.065 = 0.26$
…………..4% ของ 650 หมายถึง $\frac{4}{100}\times 650 = 26$
…………..ดังนั้น 400% ของ 0.065 น้อยกว่า 4% ของ 650 อยู่ 26 – 0.26 = 25.74

ตัวอย่างที่ 2 จงหาว่า 2% ของ 5% ของ 6% ของ 1,000,000 คิดเป็นกี่เปอร์เซ็นต์ของ 240
วิธีทำ…….2% ของ 5% ของ 6% ของ 1,000,000 หมายถึง $\frac{2}{100}\times \frac{5}{100}\times \frac{6}{100}\times 1,000,000 = 60$
………….. 60 คิดเป็นกี่เปอร์เซ็นต์ของ 420 จะได้ $\frac{60}{240}\times 100 = 25$
…………. ดังนั้น 2% ของ 5% ของ 6% ของ 1,000,000 คิดเป็น 25 % ของ 240

ตัวอย่างที่ 3 นักเรียนชั้น ม.1 ของโรงเรียนแห่งหนึ่งสอบได้ 84% มีนักเรียนสอบได้มากกว่าสอบตก 663 คน อยากทราบว่า นักเรียนชั้น ม.1 ของโรงเรียนแห่งนี้มีกี่คน
วิธีทำ…..นักเรียนชั้น ม.1 สอบได้ 84% หมายความว่า ถ้ามีนักเรียนม.1 จำนวน 100 คน จะมีนักเรียนสอบได้ 84 คน และสอบตก 100-84 = 16 คน
……….. ดังนั้น จึงมีนักเรียนสอบได้มากกว่าสอบตก 84 – 16 = 68 8o
……….. มีนักเรียนสอบได้มากกว่าสอบตก 68 คน จากนักเรียนทั้งหมด 100 คน
……….. ถ้ามีนักเรียนสอบได้มากกว่าสอบตก 663 คน จะมีนักเรียนทั้งหมด $\frac{100}{68}\times 663 = 975$ คน
……….. ดังนั้น นักเรียนชั้น ม.1 ของโรงเรียนแห่งนี้มี 975 คน

ตัวอย่างที่ 4 ถ้ารูปสี่เหลี่ยมจัตุรัสรูปหนึ่งเปลี่ยนแปลงไปเป็นรูปสี่เหลี่ยมผืนผ้า โดยมีด้านหนึ่งยาวเพิ่มขึ้นร้อยละ 60 อีกด้านหนึ่งยาวลดลงร้อยละ 60 แล้ว ถามว่ารูปสี่เหลี่ยมผืนผ้าจะมีพื้นที่เปลี่ยนแปลงจากรูปสี่เหลี่ยมจัตุรัสอย่างไร
วิธีทำ…..สมมติให้ ความยาวแต่ละด้านของสี่เหลี่ยมจัตุรัสเดิมยาวด้านละ 10 หน่วย มีพื้นที่ 10 × 10 = 100 ตารางหน่วย
………… 60% ของความยาวเดิม หมายถึง $\frac{60}{100}\times 10 = 6$
……….. จะได้สี่เหลี่ยมผืนผ้า ยาว 10+6 = 16 หน่วย และกว้าง 10 – 6 = 4 หน่วย
……….. ดังนั้น พื้นที่ของรูปสี่เหลี่ยมผืนผ้าใหม่ เป็น 16 × 4 = 64 ตารางหน่วย
……….. สรุปได้ว่า สี่เหลี่ยมใหม่มีพื้นที่ลดลงจากเดิม 100 – 64 = 36 ตารางหน่วย หรือ ลดลงจากเดิม 36 %

ตัวอย่างที่ 5 ปากกา 1,800 ด้าม เป็นปากกาสีน้ำเงิน ปากกาสีดำ และปากกาสีแดง นำมาจัดวางขายบนชั้น โดยเป็นปากกาสีน้ำเงิน 65% ของปากกาทั้งหมด และเป็นปากกาสีดำ 15% ของทั้งหมด ที่เหลือเป็นปากกาสีแดง ต่อมาขายปากกาสีน้ำเงินไปจำนวนหนึ่ง แล้วนับปากกาทั้งหมดใหม่ พบว่าเป็นปากกาสีน้ำเงินอยู่ 55% ของปากกาที่เหลืออยู่บนชั้น อยากทราบว่าจะเหลืออปากกาสีน้ำเงินกี่ด้าม
วิธีทำ…..เดิมมีปากกาสีน้ำเงิน $\frac{65}{100}\times 1,800 = 1,170$ ด้าม
……….ขายปากกาสีน้ำเงินไป..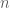 $n$ ..ด้าม เหลือปากกาสีน้ำเงิน $1,170-n$ ด้าม
……….และมีปากกาเหลือทั้งหมด $1,800-n$ ด้าม
………..ดังนั้น อัตราส่วนของ ปากกาน้ำเงินเหลือ : ปากกาที่เหลือบนชั้น เป็น $\frac{1,170-n}{1,800-n} = \frac{55}{100}$
…………..แก้สมการได้ … $n = 400$
……..เหลือปากกาสีน้ำเงิน $1,170 - 400 = 770$ ด้าม

…….เป็นยังไงกันบ้างครับเกี่ยวกับการคิดคำนวณ “ร้อยละของจำนวนใด” พอจะเข้าใจกันบ้างไหมครับ ลองดาวน์โหลดแบบฝึกหัดไปทำเป็นการบ้านเกี่ยวกับ “ร้อยละของจำนวนใด” ดูนะครับ ได้ผลเป็นอย่างไร ลองเขียนมาเล่าสู่กันฟังบ้าง…แล้วพบกันใหม่ครับ Bye…Bye

ค้นหาบล็อกนี้

อริสา

คณิตศาสตร์เสริม

ร้อยละของจำนวนใด

ความคิดเห็น

แสดงความคิดเห็น

โพสต์ยอดนิยมจากบล็อกนี้

ภาษาไทย

วิชาพระพุทธ