คณิตศาสตร์พื้นฐาน

บทที่ 1. ทศนิยมและเศษส่วน

ทศนิยม(Decimals)

1) ทศนิยมและการเปรียบเทียบทศนิยม

         1.1) ความหมายและรูปของทศนิยม
ทศนิยม เป็นสัญลักษณ์ที่ใช้แทนจำ นวนรูปแบบหนึ่ง ซึ่งเกิดจำกกำรหำรจำ นวนที่อยู่ในรูปเศษส่วนโดยนำ
ตัวส่วนไปหำรตัวเศษแล้วได้ผลลัพธ์ที่ไม่ลงตัว หรือเป็นกำรบอกปริมำณของสิ่งต่ำงๆที่ไม่เต็มหน่วย

รูปทศนิยม
จำ นวนที่เขียนในรูปทศนิยมจะมี ( . ) เป็นส่วนประกอบ ตัวเลขที่อยู่หน้ำจุดจะเป็นจำ นวนเต็ม ส่วนตัว
เลขที่อยู่หลังจุดเรียกว่ำ ทศนิยม

การอ่านทศนิยม
ทศนิยมประกอบด้วย 2 ส่วน ส่วนที่อยู่หน้ำจุดเป็นจำ นวนเต็มอ่ำนเช่นเดียวกันกับจำ นวนเต็มหรือ
จำ นวนนับโดยทั่วไป ส่วนที่อยู่หลังจุดจะอ่ำนทีละตัวเป็นเลขโดดตำมตัวเลขที่มี
เช่น 0.35 อ่ำนว่ำ ศูนย์จุดสำมห้า

1.2) ค่าประจาหลักและการเขียนในรูปการกระจาย
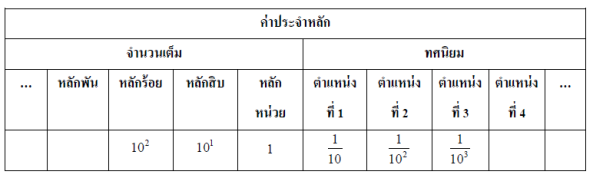
กำรเขียนทศนิยมในรูปกำรกระจำย เขียนได้ในรูปผลบวกของผลคูณระหว่ำงเลขในแต่ละหลักกับค่ำ
ประจำ หลักที่เลขโดดนั้นๆตั้งอยู่
ค่าประจาหลักของทศนิยม

1.3) ค่าสัมบูรณ์ของทศนิยม
ค่ำสัมบูรณ์ของจำ นวนใดๆหำได้จำกระยะที่จำ นวนนั้นๆอยู่ห่ำงจำก 0 บนเส้นจำ นวน

1.4) การเปรียบเทียบทศนิยม
เรำสำมำรถเปรียบเทียบทศนิยมสองจำนวนใดๆโดยใช้หลักเกณฑ์ดังต่อไปนี้
1) กำรเปรียบเทียบทศนิยมที่เป็นบวกสองจำนวนใดๆ ให้พิจำรณำเลขโดดคู่แรกในตำแหน่งเดียวกันที่ไม่เท่ำกัน
จำนวนที่มีเลขโดดในตำแหน่งนั้นมำกกว่ำจะเป็นจำนวนที่มำกกว่ำ
เช่น 2.35 ……. 3.26 3.14 …… 3.32
12.135 ……. 12.134 5.832 ……… 5.831
2) กำรเปรียบเทียบทศนิยมที่เป็นลบสองจำนวนใดๆ ให้หำค่ำสัมบูรณ์ของทั้งสองจำนวน จำนวนที่มีค่ำสัมบูรณ์
น้อยกว่ำจะเป็นจำนวนที่มำกกว่ำ
เช่น -1.83 ……. -2.85 -3.425 ……… -3.321
-5.143 ……… -5.137 -0.157 ………. -0.125
3) กำรเปรียบเทียบทศนิยมที่เป็นบวกและทศนิยมที่เป็นลบ เนื่องจำกทศนิยมที่เป็นบวกอยู่ทำงขวำของ 0
ดังนั้นทศนิยมที่เป็นบวกจะมำกกว่ำทศนิยมที่เป็นลบเสมอ

2) การบวกและการลบทศนิยม

เรำสำมำรถสรุปหลักเกณฑ์กำรบวกทศนิยมได้ดังนี้
1. กำรหำผลบวกระหว่ำงทศนิยมที่เป็นบวก ให้นำค่ำสัมบูรณ์มำบวกกันแล้วตอบเป็นจำนวนบวก
2. กำรหำผลบวกระหว่ำงทศนิยมที่เป็นลบ ให้นำค่ำสัมบูรณ์มำบวกกันแล้วตอบเป็นจำนวนลบ
3. กำรหำผลบวกระหว่ำงทศนิยมที่เป็นบวกกับทศนิยมที่เป็นลบ ให้นำค่ำสัมบูรณ์มำลบกันแล้วตอบเป็นจำนวนบวกหรือลบตำมจำนวนที่มีค่ำสัมบูรณ์มำกกว่ำ
นอกจำกนี้ เรำยังสำมำรถใช้หลักเกณฑ์เดียวกันนี้ในกำรหำผลลบของทศนิยม โดยกำรเปลี่ยนรูปกำรลบให้อยู่ในรูปกำรบวกดังนี้
ตัวตั้ง – ตัวลบ = ตัวตั้ง + จำนวนตรงข้ำมของตัวลบ
เช่น 2.13 – 1.12 = 2.13 + (-1.12 )

3) การคูณและการหารทศนิยม

การคูณทศนิยม มีหลักกำรเช่นเดียวกับกำรคูณจำ นวนเต็ม โดยกำรเปลี่ยนทศนิยมทั้งตัวตั้งและตัวคูณให้เป็น
จำ นวนเต็ม แต่จำ นวนตำ แหน่งของทศนิยมของผลลัพธ์ จะเท่ำกับผลบวกของจำ นวนตำ แหน่งของทศนิยมตัวตั้ง
และตัวคูณ

การหารทศนิยม มีหลักกำรดังนี้
1. ต้องทำ ตัวหำรให้เป็นจำ นวนเต็ม โดยกำรนำ 10 , 100 , 1000 , . . . มำคูณทั้งตัวตั้งและตัวหำร
2. ถ้ำตัวตั้งและตัวหำรเป็นทศนิยมที่เป็นบวก ให้นำ ค่ำสัมบูรณ์มำหำรกัน แล้วตอบเป็นจำ นวนบวก
3. ถ้ำตัวตั้งและตัวหำรเป็นทศนิยมที่เป็นลบ ให้นำ ค่ำสัมบูรณ์มำหำรกัน แล้วตอบเป็นจำ นวนบวก
4. ถ้ำตัวตั้งเป็นจำ นวนบวกและตัวหำรเป็นจำ นวนลบ หรือ ตัวตั้งเป็นจำ นวนลบและตัวหำรเป็นจำ นวนบวก
ให้นำ ค่ำสัมบูรณ์ของตัวตั้งและตัวหำรมำหำรกัน แล้วตอบเป็นจำ นวนลบ

เศษส่วน (Fraction)
เศษส่วน หมำถึง จำ นวนที่ใช้บอกปริมำณที่ไม่เป็นจำ นวนเต็ม ซึ่งจะเขียนในรูป a
b
เมื่อ a และ b
เป็นจำ นวนเต็ม โดยที่ b # 0
ชนิดของเศษส่วน แบ่งออกเป็นดังนี้
1) เศษส่วนแท้ หรือเศษส่วนสำมัญ หมำยถึงเศษส่วนที่มีตัวเศษน้อยกว่ำตัวส่วน
2) เศษส่วนเกิน หมำยถึง เศษส่วนที่มีตัวเศษมำกกว่ำตัวส่วน
3) เศษส่วนจานวนคละ หมำยถึง เศษส่วนที่มีจำ นวนเต็มและเศษส่วนแท้รวมอยู่ด้วยกัน

ข้อสังเกตเกี่ยวกับเศษส่วนจานวนคละ

             1) เศษส่วนจำ นวนคละสำมำรถเขียนในรูปผลบวกได้

             2) เศษส่วนจำ นวนคละสำมำรถเขียนในรูปเศษส่วนเกินได้

4) เศษส่วนซ้อน หมำยถึง เศษส่วนที่มีตัวเศษหรือตัวส่วน หรือทั้งตัวเศษและตัวส่วนเป็นเศษส่วน

เศษส่วนที่เท่ากัน
ถ้ำคูณหรือหำรตัวเศษและตัวส่วนของเศษส่วนใดๆ ด้วยจำ นวนเดียวกันที่ไม่เท่ำกับศูนย์ แล้ว ผลลัพธ์ที่ได้จะเป็น
เศษส่วนที่เท่ำกับเศษส่วนจำ นวนเดิม กล่ำวคือ ถ้ำ a
b
เป็นเศษส่วน และ c เป็นจำ นวนใดๆ ที่ c  0

การเปรียบเทียบเศษส่วน
ในกำรเปรียบเทียบเศษส่วนไม่ว่ำจะเป็นเศษส่วนที่เป็นบวกหรือเศษส่วนที่เป็นลบ ขั้นแรกจะต้องทำ ตัวส่วนของ
เศษส่วนให้เป็นจำ นวนเต็มบวกก่อน แล้วจึงพิจำรณำดังนี้
1) เมื่อตัวส่วนของเศษส่วนนั้นเท่ำกัน ให้พิจำรณำตัวเศษ กล่ำวคือ ถ้ำตัวเศษเท่ำกันแล้วเศษส่วนทั้งสองจะมีค่ำ
เท่ำกัน แต่ถ้ำตัวเศษไม่เท่ำกัน ให้พิจำรณำว่ำตัวเศษของเศษส่วนใดมีค่ำมำกกว่ำ แล้วเศษส่วนนั้นจะมีค่ำ
มำกกว่ำ
2) เมื่อตัวส่วนของเศษส่วนทั้งสองนั้นไม่เท่ำกัน ให้ทำ ตัวส่วนของเศษส่วนทั้งสองเป็นเศษส่วนที่มีตัวส่วน
เท่ำกัน แล้วเปรียบเทียบตัวเศษดังที่กล่ำวแล้วในข้อ 1)

การบวกและการลบเศษส่วน มีหลักกำรในกำรพิจำรณำดังนี้
1) เขียนเศษส่วนให้อยู่ในรูป a
b
เมื่อ a และ b เป็นจำ นวนเตม็ ที่ b  0
2) ถ้ำตัวส่วนเท่ำกัน ให้นำ ตัวเศษมำบวกหรือลบกัน และตัวส่วนมีค่ำเท่ำเดิม
3) ถ้ำตัวส่วนมีค่ำไม่เท่ำกัน ให้ทำ ตัวส่วนให้เท่ำกัน ซึ่งโดยทั่วไปจะทำ ตัวส่วนให้เท่ำกับ ค.ร.น. ของตัวส่วนทุก
ตัว จำกนั้นนำ เศษมำบวกหรือลบกัน และตัวส่วนมีค่ำเท่ำเดิม

การคูณและการหารเศษส่วน
การคูณเศษส่วน เป็นเศษส่วนที่ b และ d ไม่เท่ำกับศูนย์ ผลคูณของ a

หลักเกณฑ์กำรคูณจำ นวนเต็มและข้อตกลง
การหารเศษส่วน มีหลักกำรดังนี้
1) ถ้ำเป็นเศษส่วนจำ นวนคละให้เปลี่ยนเป็นเศษส่วนเกิน
2) เปลี่ยนเครื่องหมำยหำรเป็นเครื่องหมำยคูณ แล้วเปลี่ยนตัวหำรโดยกลับเศษเป็นส่วน กลับส่วนเป็นเศษ ดังนี้